Cara Menghitung Skor-Z Menggunakan Microsoft Excel

Z-Score adalah nilai statistik yang memberi tahu Anda berapa banyak standar deviasi dari nilai tertentu yang terjadi dari rata-rata seluruh kumpulan data. Anda dapat menggunakan rumus AVERAGE dan STDEV.S atau STDEV.P untuk menghitung rata-rata dan standar deviasi data Anda dan kemudian menggunakan hasil tersebut untuk menentukan Z-Score dari setiap nilai.

Apa yang dimaksud dengan Z-Score dan apa yang dilakukan fungsi AVERAGE, STDEV.S, dan STDEV.P?

Z-Score adalah cara sederhana untuk membandingkan nilai dari dua set data yang berbeda. Ini didefinisikan sebagai jumlah standar deviasi dari rata-rata titik data terletak. Rumus umum terlihat seperti ini:

= (DataPoint-AVERAGE (DataSet)) / STDEV (DataSet)

Berikut ini contoh untuk membantu memperjelas. Katakanlah Anda ingin membandingkan hasil tes dua siswa Aljabar yang diajarkan oleh guru yang berbeda. Anda tahu siswa pertama mendapat 95% pada ujian akhir dalam satu kelas, dan siswa di kelas lain mendapat nilai 87%.

Sekilas, nilai 95% lebih mengesankan, tetapi bagaimana jika guru kelas dua memberikan ujian yang lebih sulit? Anda dapat menghitung Z-Score dari skor masing-masing siswa berdasarkan skor rata-rata di setiap kelas dan standar deviasi skor di setiap kelas. Membandingkan Skor Z dari kedua siswa dapat mengungkapkan bahwa siswa dengan skor 87% melakukan lebih baik dibandingkan dengan seluruh kelas mereka daripada siswa dengan skor 98% dibandingkan dengan sisa kelas mereka.

Nilai statistik pertama yang Anda butuhkan adalah fungsi 'rata-rata' dan “AVERAGE” Excel menghitung nilai itu. Ini hanya menambah semua nilai dalam rentang sel dan membagi jumlah itu dengan jumlah sel yang mengandung nilai numerik (mengabaikan sel kosong).

Nilai statistik lain yang kita butuhkan adalah 'standar deviasi' dan Excel memiliki dua fungsi berbeda untuk menghitung standar deviasi dengan cara yang sedikit berbeda.

Versi Excel sebelumnya hanya memiliki fungsi "STDEV", yang menghitung deviasi standar sambil memperlakukan data sebagai 'sampel' populasi. Excel 2010 memecahnya menjadi dua fungsi yang menghitung standar deviasi:

STDEV.S: Fungsi ini identik dengan fungsi "STDEV" sebelumnya. Ini menghitung deviasi standar sambil memperlakukan data sebagai 'sampel' populasi. Sampel populasi mungkin seperti nyamuk tertentu yang dikumpulkan untuk proyek penelitian atau mobil yang disisihkan dan digunakan untuk pengujian keselamatan kecelakaan..
STDEV.P: Fungsi ini menghitung deviasi standar sambil memperlakukan data sebagai seluruh populasi. Seluruh populasi akan menjadi sesuatu seperti semua nyamuk di Bumi atau setiap mobil dalam menjalankan produksi model tertentu.

Yang Anda pilih didasarkan pada kumpulan data Anda. Perbedaannya biasanya kecil, tetapi hasil dari fungsi "STDEV.P" akan selalu lebih kecil dari hasil fungsi "STDEV.S" untuk set data yang sama. Ini adalah pendekatan yang lebih konservatif untuk menganggap ada lebih banyak variabilitas dalam data.

Mari Kita Lihat Contoh

Sebagai contoh kami, kami memiliki dua kolom ("Nilai" dan "Skor-Z") dan tiga sel "pembantu" untuk menyimpan hasil fungsi "AVERAGE," "STDEV.S," dan "STDEV.P". Kolom "Nilai" berisi sepuluh angka acak yang berpusat di sekitar 500, dan kolom "Z-Score" adalah tempat kami akan menghitung Z-Score menggunakan hasil yang disimpan dalam sel 'helper'.

Pertama, kita akan menghitung nilai rata-rata menggunakan fungsi “RATA-RATA”. Pilih sel tempat Anda akan menyimpan hasil dari fungsi "AVERAGE".

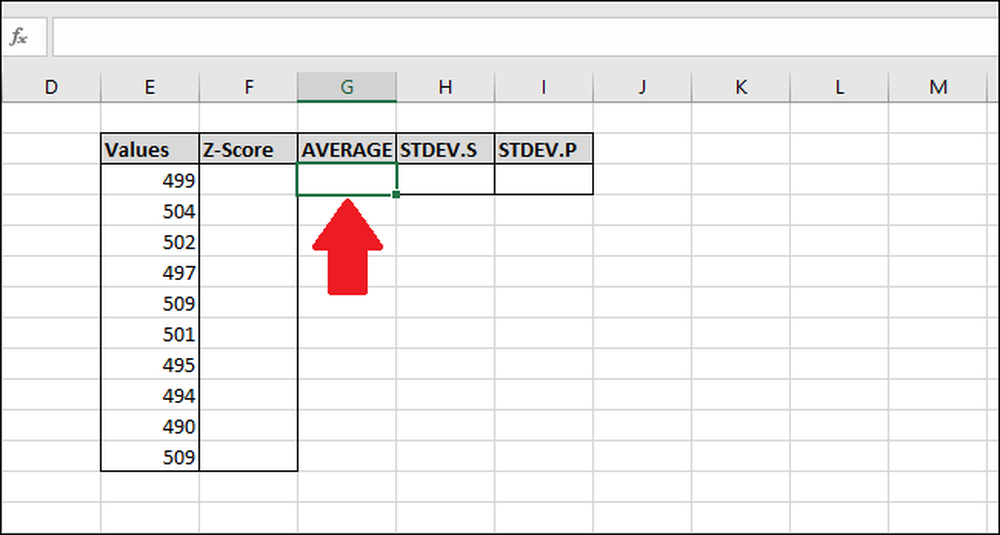
Ketikkan rumus berikut dan tekan memasukkan -atau- gunakan menu "Formula".

= AVERAGE (E2: E13)

Untuk mengakses fungsi melalui menu "Rumus", pilih tarik-turun "Fungsi Lainnya", pilih opsi "Statistik", lalu klik "RATA-RATA."

Di jendela Function Arguments, pilih semua sel di kolom "Nilai" sebagai input untuk bidang "Number1". Anda tidak perlu khawatir tentang bidang "Number2".

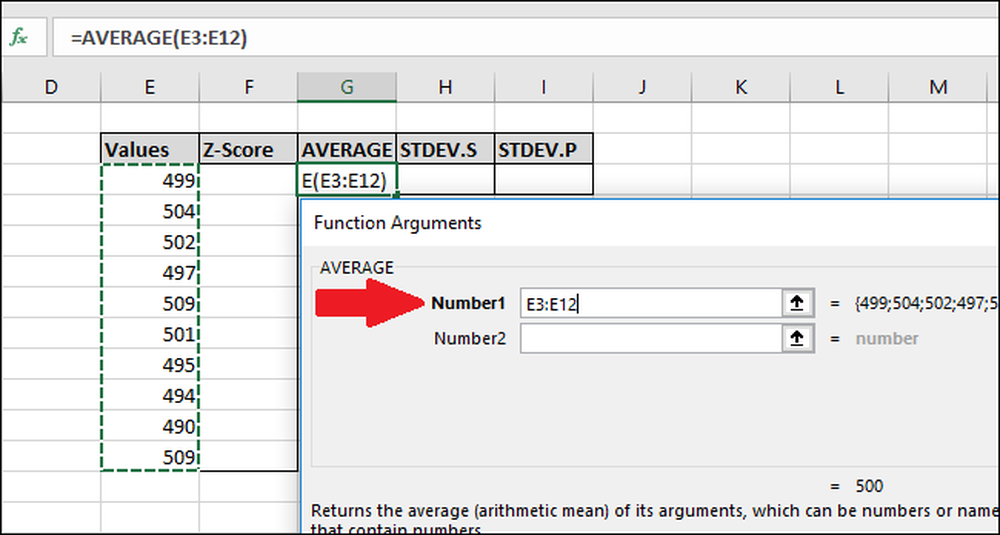
Sekarang tekan "OK."

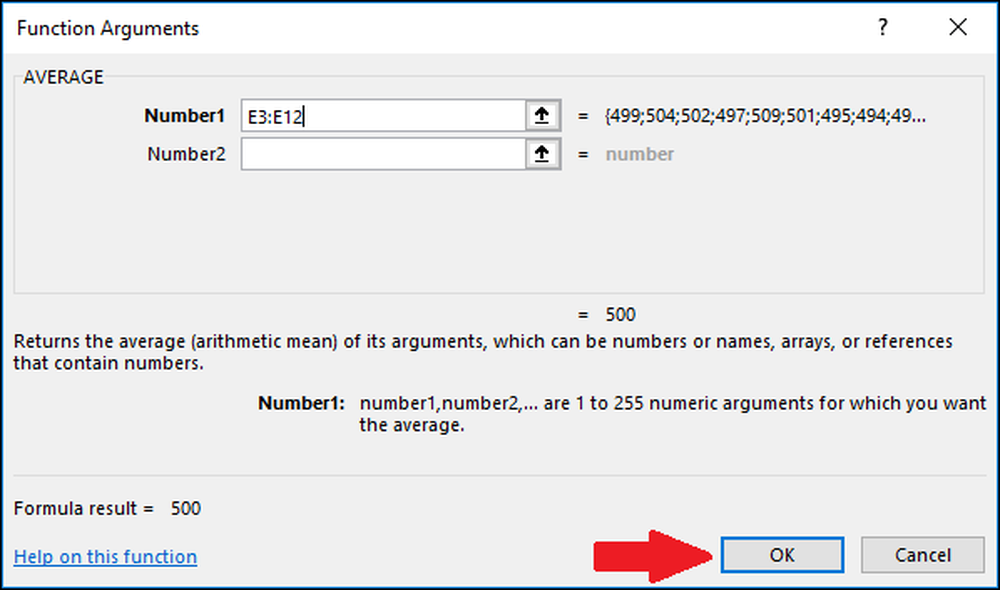
Selanjutnya, kita perlu menghitung standar deviasi dari nilai-nilai menggunakan fungsi "STDEV.S" atau "STDEV.P". Dalam contoh ini, kami akan menunjukkan kepada Anda cara menghitung kedua nilai, dimulai dengan "STDEV.S." Pilih sel tempat hasil akan disimpan.

Untuk menghitung deviasi standar menggunakan fungsi "STDEV.S", ketikkan rumus ini dan tekan Enter (atau akses melalui menu "Rumus").

= STDEV.S (E3: E12)

Untuk mengakses fungsi melalui menu "Rumus", pilih tarik-turun "Fungsi Lainnya", pilih opsi "Statistik", gulirkan sedikit ke bawah, lalu klik perintah "STDEV.S".

Di jendela Function Arguments, pilih semua sel di kolom "Nilai" sebagai input untuk bidang "Number1". Anda juga tidak perlu khawatir tentang bidang "Number2".

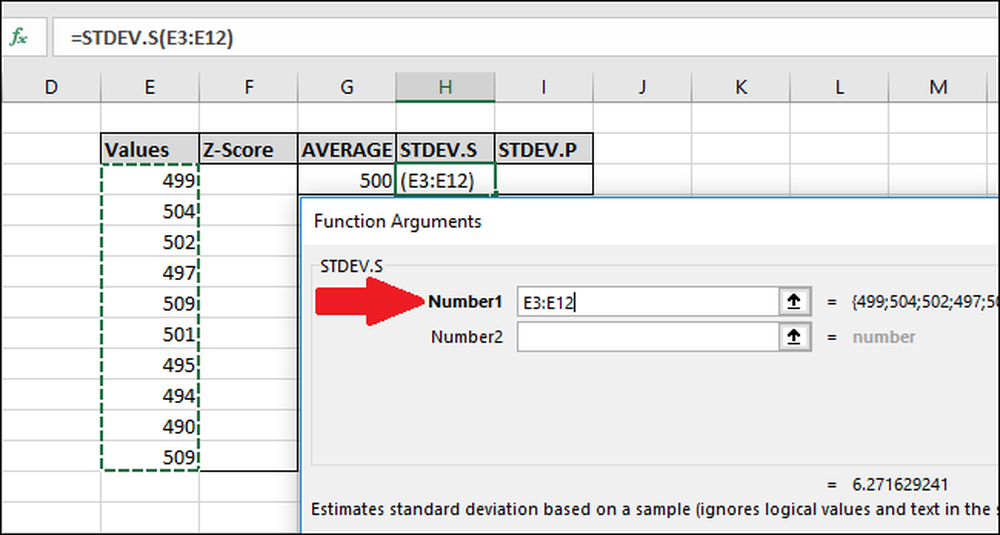
Sekarang tekan "OK."

Selanjutnya, kita akan menghitung deviasi standar menggunakan fungsi "STDEV.P". Pilih sel tempat hasil akan disimpan.

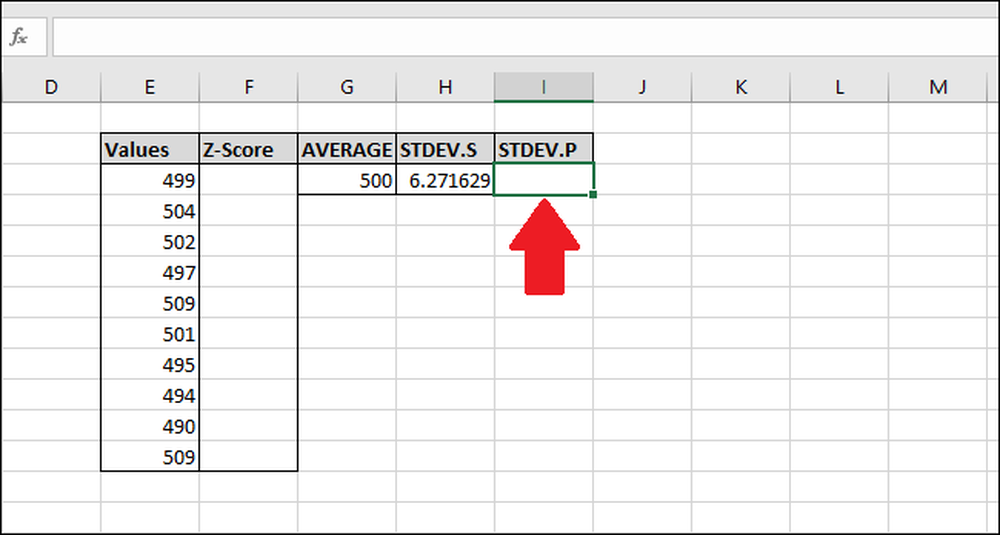
Untuk menghitung standar deviasi menggunakan fungsi "STDEV.P", ketikkan rumus ini dan tekan Enter (atau akses melalui menu "Formula").

= STDEV.P (E3: E12)

Untuk mengakses fungsi melalui menu "Rumus", pilih tarik-turun "Fungsi Lainnya", pilih opsi "Statistik", gulirkan sedikit ke bawah, lalu klik rumus "STDEV.P".

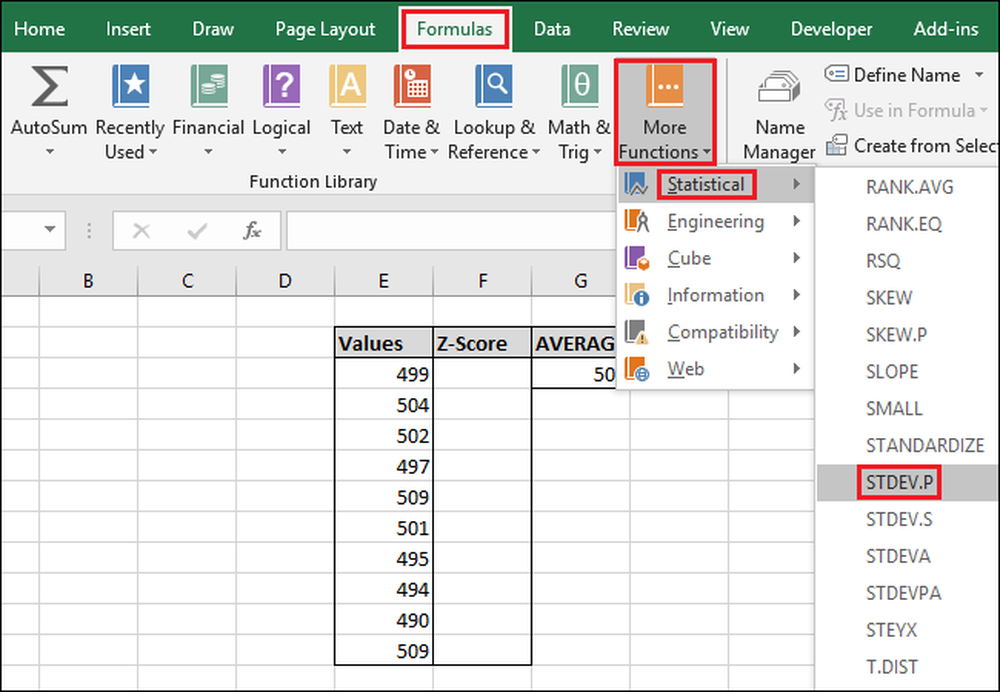
Di jendela Function Arguments, pilih semua sel di kolom "Nilai" sebagai input untuk bidang "Number1". Sekali lagi, Anda tidak perlu khawatir tentang bidang "Number2".

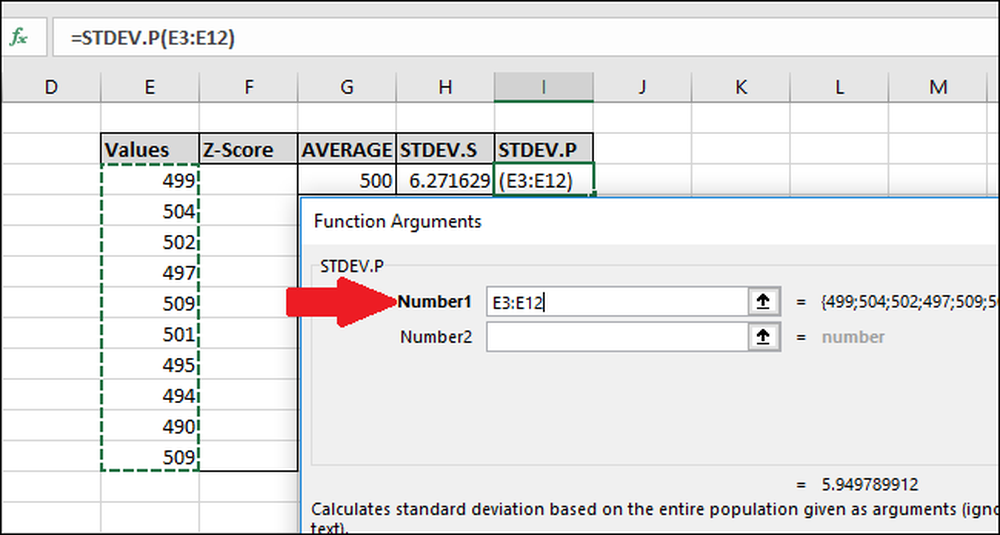
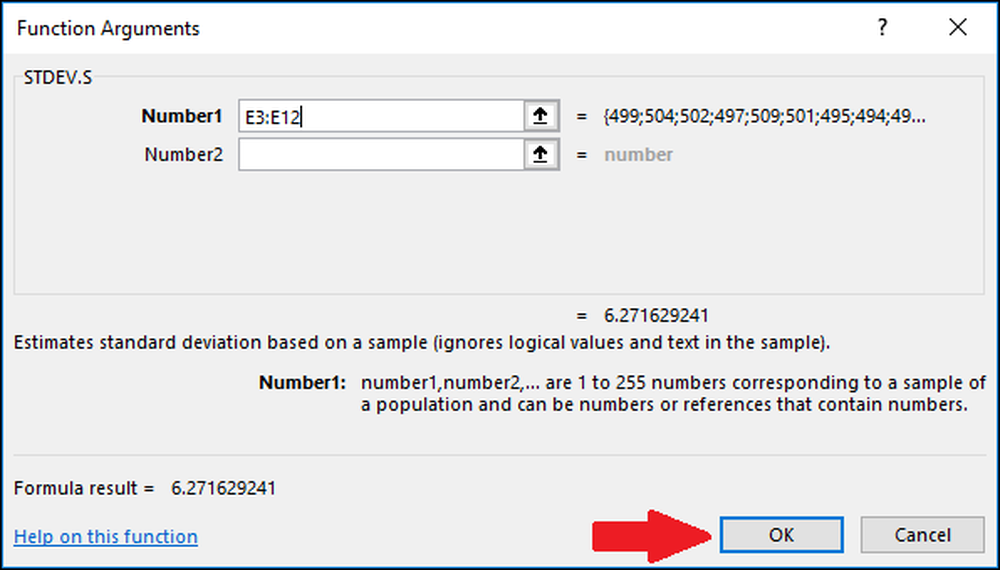
Sekarang tekan "OK."

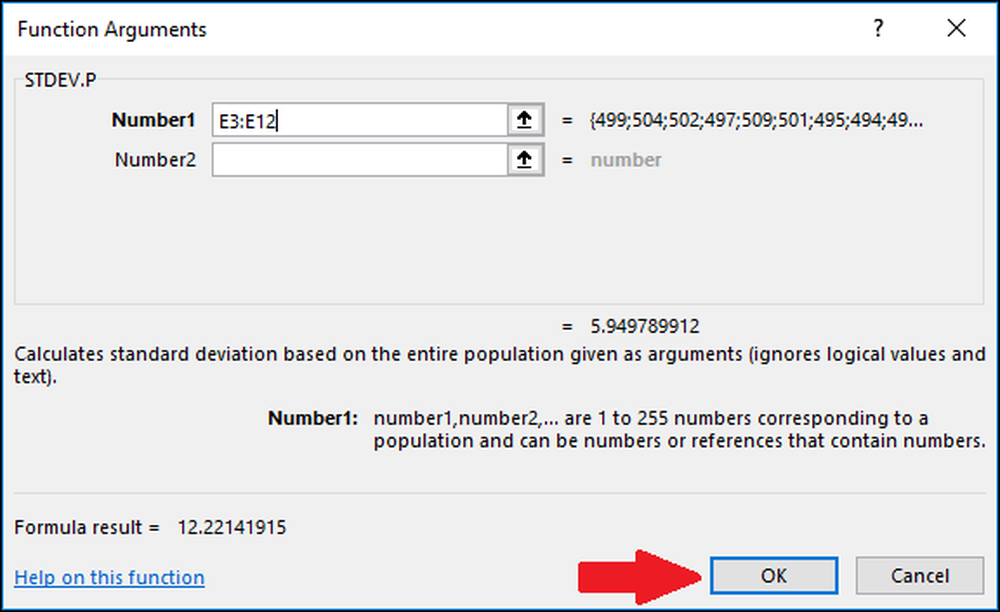
Sekarang kami telah menghitung rata-rata dan standar deviasi data kami, kami memiliki semua yang kami butuhkan untuk menghitung Z-Score. Kita bisa menggunakan rumus sederhana yang mereferensikan sel yang berisi hasil dari "AVERAGE" dan "STDEV.S" atau "STDEV.P" fungsi.

Pilih sel pertama di kolom "Z-Score". Kami akan menggunakan hasil dari fungsi "STDEV.S" untuk contoh ini, tetapi Anda juga bisa menggunakan hasil dari "STDEV.P."

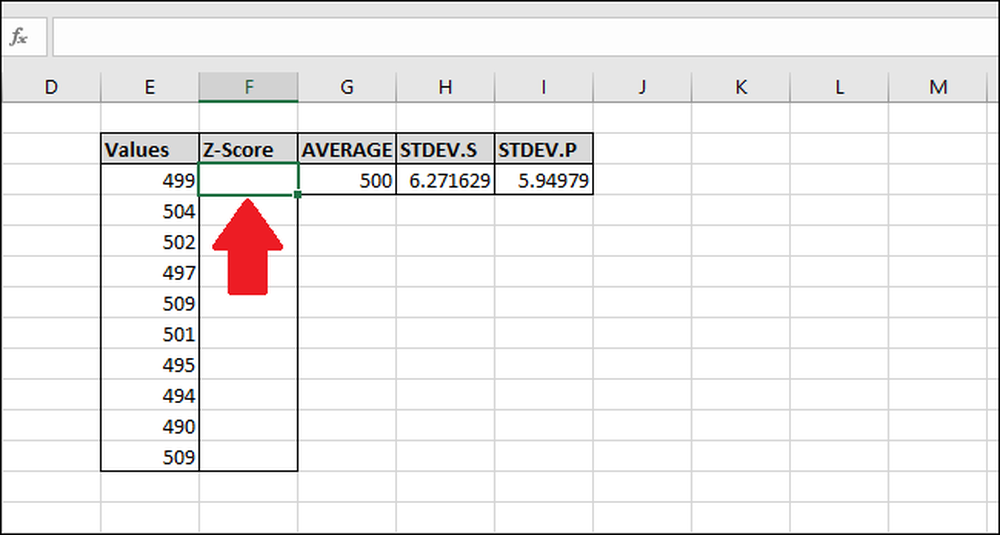
Ketik rumus berikut dan tekan Enter:

= (E3- $ G $ 3) / $ H $ 3

Atau, Anda bisa menggunakan langkah-langkah berikut untuk memasukkan rumus alih-alih mengetik:

Klik sel F3 dan ketik = (
Pilih sel E3. (Anda dapat menekan tombol tombol panah kiri satu kali atau gunakan mouse)
Ketikkan tanda minus -
Pilih sel G3 lalu tekan F4 untuk menambahkan "$" karakter untuk membuat referensi 'absolut' ke sel (itu akan menggilir "G3"> "$G$3 ">" G$3 ">"$G3 ">" G3 "jika Anda terus menekan F4)
Mengetik ) /
Pilih sel H3 (atau I3 jika Anda menggunakan "STDEV.P") dan tekan F4 untuk menambahkan dua karakter "$".
tekan enter

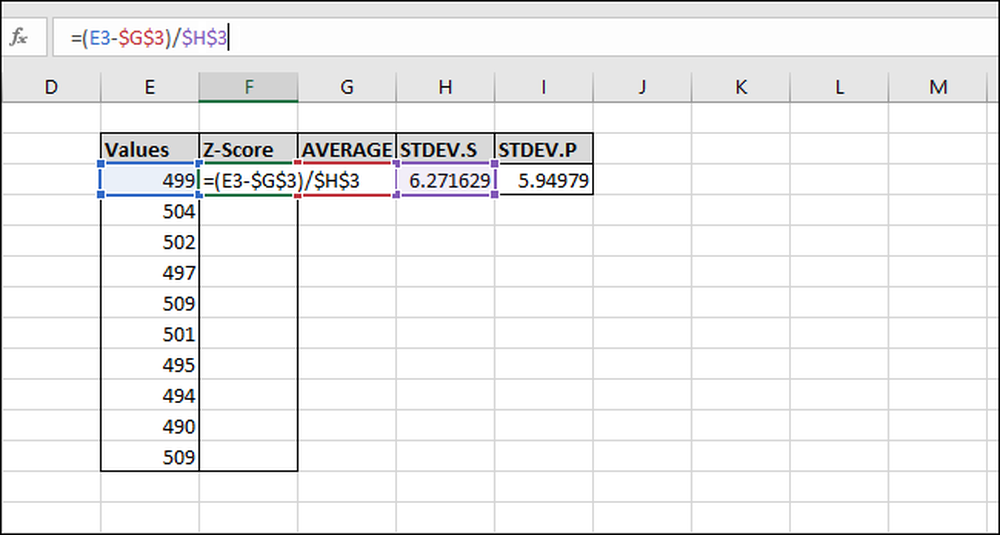
Z-Score telah dihitung untuk nilai pertama. Itu adalah 0,15945 standar deviasi di bawah rata-rata. Untuk memeriksa hasilnya, Anda dapat mengalikan deviasi standar dengan hasil ini (6.271629 * -0.15945) dan memeriksa bahwa hasilnya sama dengan perbedaan antara nilai dan rata-rata (499-500). Kedua hasil sama, sehingga nilainya masuk akal.

Mari kita hitung Skor-Z dari sisa nilai. Sorot seluruh kolom 'Skor-Z' yang dimulai dengan sel yang berisi rumus.

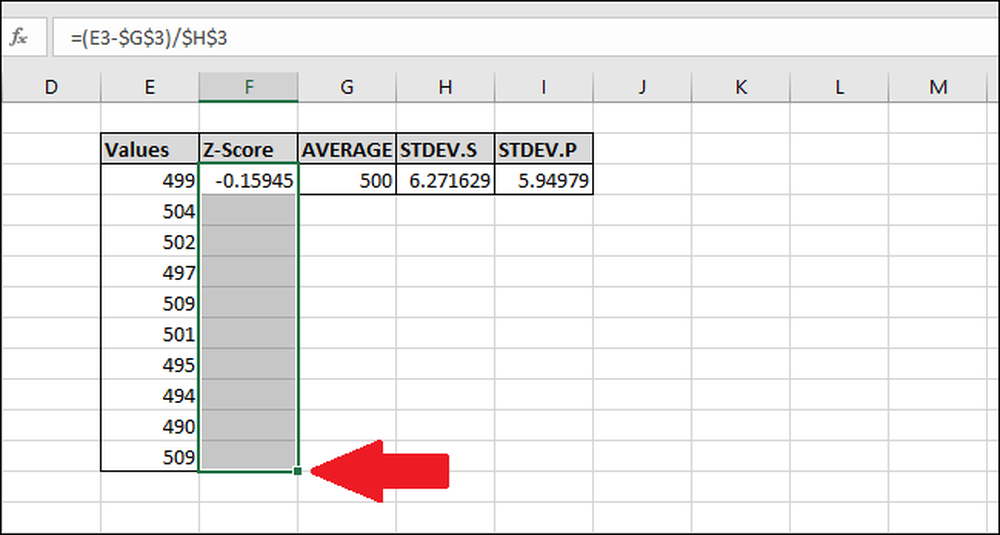
Tekan Ctrl + D, yang menyalin rumus di sel atas ke bawah melalui semua sel yang dipilih lainnya.

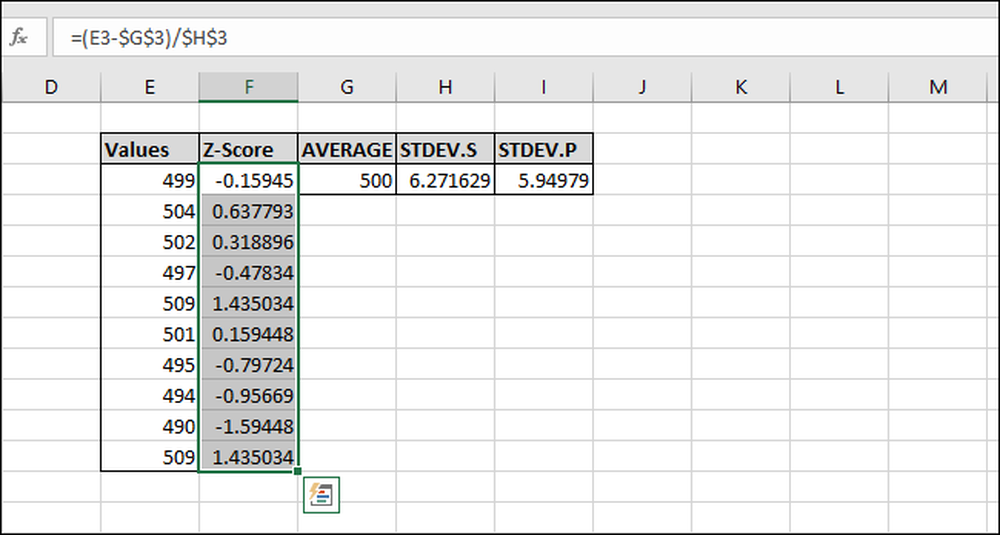
Sekarang rumus telah 'diisi-turun' ke semua sel, dan masing-masing akan selalu merujuk sel "AVERAGE" dan "STDEV.P" atau "STDEV.P" yang benar karena karakter "$". Jika Anda mendapatkan kesalahan, kembali dan pastikan karakter "$" termasuk dalam formula yang Anda masukkan.

Menghitung Skor-Z tanpa menggunakan Sel 'Penolong'

Sel-sel pembantu menyimpan hasil, seperti sel-sel yang menyimpan hasil dari fungsi "AVERAGE," "STDEV.S," dan "STDEV.P". Mereka bisa bermanfaat tetapi tidak selalu perlu. Anda dapat melewatkan semuanya saat menghitung Skor-Z dengan menggunakan rumus umum berikut ini sebagai gantinya.

Inilah yang menggunakan fungsi "STDEV.S":

= (Nilai-RATA-RATA (Nilai)) / STDEV.S (Nilai)

Dan satu menggunakan fungsi "STEV.P":

= (Nilai-RATA-RATA (Nilai)) / STDEV.P (Nilai)

Saat memasukkan rentang sel untuk "Nilai" dalam fungsi, pastikan untuk menambahkan referensi absolut ("$" menggunakan F4) sehingga ketika Anda 'mengisi' Anda tidak menghitung rata-rata atau standar deviasi dari rentang yang berbeda sel dalam setiap formula.

Jika Anda memiliki kumpulan data besar, mungkin akan lebih efisien untuk menggunakan sel pembantu karena tidak menghitung hasil dari "RATA-RATA" dan "STDEV.S" atau "STDEV.P" berfungsi setiap kali, menghemat sumber daya prosesor dan mempercepat waktu yang diperlukan untuk menghitung hasil.

Juga, "$ G $ 3" membutuhkan lebih sedikit byte untuk disimpan dan lebih sedikit RAM untuk dimuat daripada "AVERAGE ($ E $ 3: $ E $ 12).". Ini penting karena versi standar 32-bit Excel terbatas pada 2GB RAM (versi 64-bit tidak memiliki batasan berapa banyak RAM yang dapat digunakan).